Learning (2) - 파라미터 학습
파라미터 학습
가장 쉬운 학습 알고리즘은 여러 개의 파라미터들의 값을 바꾸는 것.
steering 알고리즘이나, 길찾기 알고리즘등에서 사용되는 magic number가 대표적인 예이다.
의사 결정 확률등을 조금 변화시키는 것도 AI동작을 크게 다르게 할 수 있다.
이처럼 파라미터들은 학습하기 좋은 대상이다.
파라미터 그래프

파라미터를 학습할 때, 파라미터 값에 따라 점수를 매길 수 있어야 한다. 점수는 AI에서 해당 파라미터 값이 얼마나 좋은지를 의미한다.
파라미터가 단 하나라면 위 그림처럼 2차원 그래프가 나오겠지만 파라미터가 여러 개라면 다 차원의 그래프가 나올 수 있다. 이런 경우 파라미터 값들의 집합에 따라 점수를 매길 수 있다.
파라미터 학습하기
만약 점수와 값의 그래프가 미분 가능하다면, 그냥 수학적으로 최적해를 계산해 낼 수 있을 것이다. 그러나 현실에서 이런 케이스는 잘 없다. 따라서 아래에 설명할 기법을 사용하는데, 이런 기법들로 학습된 값들 역시 최적해라고 할 수는 없다. 그러나 학습된 값들이 적절하게 쓸만하다면 최적해를 찾느라 노력하는 대신 그냥 이 값들을 쓰기로 할 수 있다.
Hill Climbing
초기 값을 계산한 다음, 최적해를 향해서 점점 나아가는 방법.
- 우선 초기 지점을 임의로 잡은 다음
- 파라미터 집합에 속한 각각의 파라미터 값들을 하나씩 미리 정해진 값인 STEP만큼 바꿔본 다음
- 가장 좋은 점수를 받은 파라미터 셋으로 교체한다.
- 위 과정을 주어진 횟수만큼이나, 더 이상 점수가 높아지지 않을 때까지 반복한다.
위 방법에는 큰 문제가 있는데,

학습의 결과가 local optimum(local maximum) 으로 수렴할 수 있기 때문이다.
따라서 다음과 같은 몇 가지 기법을 추가로 적용할 수 있다.
모멘텀
모멘텀은 말 그대로 진행 방향에 관성을 더하는 것이다. 즉, 일시적으로 점수가 나빠 지더라도 왔던 방향으로 계속 진행하다가 계속 점수가 좋아지지 않으면 다시 돌아오는 방법.
적응형 해법
위에서 STEP 만큼 파라미터 값을 바꿔본다고 했는데 STEP이 크다면 최적해를 지나치게 되어 학습이 끝나지 않게 되고, 작다면 학습이 오래 걸리게 된다.
따라서, 만약 한 반복에서 지금보다 더 나은 파라미터 셋을 찾았다면 STEP의 크기를 증가시켜 여러 셋들을 둘러볼 수 있게 하고, 더 나은 파라미터 셋을 찾지 못했다면 오버슈팅이 일어난 것으로 간주하여 STEP의 값을 감소시킬 수 있다.
여러 번 시도하기
단순하게 초기 값을 다 다르게 하여 여러번 시도해보는 방법.
Annealing
이 기법은 전반적으로 Hill Climbing과 유사하지만 '온도(에너지)'라는 한 가지 개념이 더 추가된다.
이름처럼 담금질을 할 때, 초반에는 온도가 높았다가 점점 떨어지는 것 처럼, 이 기법의 온도도 학습 시작 초기에는 높았다가 점차 낮아지게 된다.
이런 온도는 파라미터 셋을 평가한 점수에 더해지게 된다. (그냥 더해지는 것은 아니고, 온도만큼의 랜덤 구간을 갖는다.)
따라서 초반에는 여러 셋들을 둘러볼 수 있게 한 다음, 나중에는 한 곳으로 수렴하도록 하는 것.
더 간단한 방법
지금까지의 Annealing을 포함한 Hill Climbing은, 파라미터 셋들에 속한 모든 값들을 하나씩 움직여 본 다음 최선을 선택하는 것을 반복한다.
그러나 더 간단한 방법으로 그냥 지금보다 더 높은 점수이기만 하면 선택하는 방식을 채택할 수 있다. (그러나 결국 반복 횟수가 증가할 태니까 잘 조율하는 것이 중요하겠지?)
이런 방식을 사용할 때 Annealing을 사용한다면 개별 파라미터에 더해지는 온도 값 때문에 학습 효율이 떨어질 수 있음. 따라서 '더 나은 점수일수록 더 높은 확률로 선택'될 수 있도록 해야한다.
이런 경우 볼츠만 분포(에너지와 온도에 따른 분포)를 이용할 수 있다.(;;)
어렵지 않다. 그냥 온도가 높으면 확률이 높고, 에너지가 높으면 확률이 낮다. 라는 개념을 사용하면 된다.
이 때 에너지는 지금 계산중인 값에서 원래 가지고있던 값을 빼주면 된다.
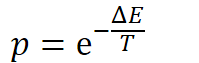
그리고 이 값이 random(0,1)보다 크다면 해당 파라미터 셋을 채택할 수 있다.
Annealing 기법에서도 모멘텀과 적응형 해법을 쓸 수 있는데, 모멘텀은 크게 효과보기가 어렵고 적응형 해법은 쓸만하다고 한다.
참고 : Ian Millington, AI for GAMES 3rd edition, CRC press, [chapter 7.2]
