인공 신경망
기초
인공 신경망의 핵심은 한 네트워크에 있는 인공 뉴런들이 다른 인공 뉴런의 부분 집합과 상호작용 하는 것이다.
mulit layer perceptron(MLP)은 인공 신경망 아키텍쳐 중 하나인데, perceptron은 인공 신경망에서 사용되는 인공 뉴런을 뜻한다. MLP는 이전 레이어의 모든 노드로부터 인풋을 받아 다음 레이어에 있는 모든 노드에 아웃풋을 전달한다. 이런 네트워크를 feedfoward 네트워크라 부른다.
프로그래머로부터 입력을 받는 레이어를 input layer로, 그리고 네트워크를 통해 쓸만한 정보를 출력하는 레이어를 output layer라 부른다.
feedfoward 네트워크 내부의 레이어들끼리 루프가 있을 수 있는데 이런 경우 recurrent network라 부르며, 매우 복잡하고 불안정하다.
뉴런 알고리즘
perceptron 알고리즘은 아래와 같이 다른 perceptron으로 부터 받은 신호에 가중치를 곱하여 더한 뒤, 일정한 역치에 따라 아웃풋을 출력한다.
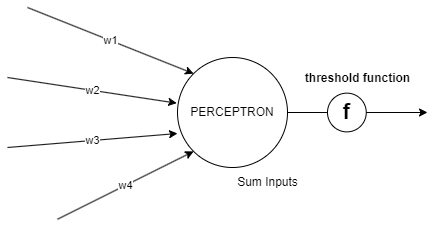
출력 값은 역치 함수(threshold function)을 적용하여 처리한다.
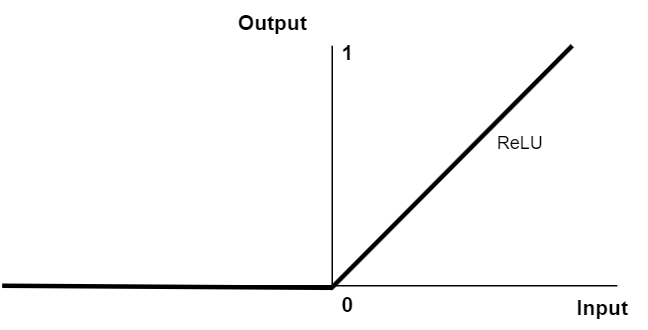
역치 함수(threshold functino)은 보통 ReLU(rectified linear unit)을 많이 쓴다.
$$f(x) = max(0,x)$$
혹은 softplus라고도 불리는 좀 더 매끄러운? 버전의 함수를 쓰기도 한다.
$$f(x) = log(1+e^x)$$
옛날에는 sigmoid를 썻는데 요즘은 작은 네트워크에서나 종종 쓰며 ReLU가 거의 대체했다.
ReLU의 한계점은 상한선이 없다는 것이며. 그래서 간혹 학습이 막힐 수 있음.
문제
Decision Tree나 Fuzzy State machine같은 방식은 다양한 상황을 커버하기 어렵다. Decision Tree Learning도 마찬가지. Decision Tree는 정확하나, 오히려 그런 면 때문에 학습한 방식 이외의 상황을 잘 처리하지 못한다. 반면 인공 신경망은 부정확하다. 그러나 학습한 방식 이외의 상황을 extrapolating으로 꽤 처리한다.
따라서 게임 AI에 어떤 방식을 사용할지를 정할 때는, 정확성과 일반화 두개를 잘 저울질 해봐야 한다.
학습
보통 네트워크 학습은 어떤 뉴런 알고리즘을 사용하는지와 무관하다. 네트워크 학습은 각 perceptron에서 이전 perceptron들의 출력에 곱해지는 가중치를 학습하는 것으로, 이는 곧 어떤 것이 정답에 연관있는지를 판별하는 것을 학습하는 것이다. 그러나 이런 판별은 어려운데, 특히 intermediate layer(input과 output을 제외한 레이어)를 많이 가지고 있을 수록 어렵다. 이런 문제를 credit assigment problem이라고 하며, 모든 상황에 통용되는 뾰족한 해결법은 없다.
가중치를 학습할 때는 Feedforward와 Backpropagation을 수행한다. 실질적으로 가중치가 변하는 부분은 Backpropagation
Feedforward
이전 노드들로부터 인풋을 받아 다음 노드들에게 아웃풋을 전달하는 것. 인풋에 가중치를 적용해서 더하고, 역치 함수를 적용한 뒤 아웃풋을 생성하는 것.
Backpropagation
이건 다시 결과를 토대로 이전 노드들에게 피드백을 전달하는 방식임. 우선 가장 이상적인 아웃풋은 원하는 아웃풋을 제외한 모든 아웃풋 노드들의 값이 0인 경우임. 어쨋든 이런 피드백을 "에러"라고 부를 수 있는데 이 값이 음수이면 관련된 노드들의 가중치를 줄이고, 이 값이 양수이면 관련된 노드들의 가중치를 증가시킨다.
backpropagation에서 가중치를 업데이트 하는 수식은 다음과 같다. 뉴런들의 상태를 i,j 가 각각 뉴런일 때, $\omicron_j$는 뉴런 j의 상태를, $\delta_j$를 에러, $\eta$는 gain, 그리고 $w_{ij}$는 i와j사이의 연결 강도(가중치)를 의미한다.
$$w'_{ij} = w_{ij} + \eta \delta_j \omicron_i $$
에러는 노드가 속해있는 레이어가 아웃풋 레이어냐 히든 레이어냐에 따라 다르다.
아웃풋 노드라면 아래와 같이 계산하며 $t_j$는 정답이 되는 값이다.
$$\delta_j = \omicron_j (1-\omicron_j)(t_j - \omicron_j)$$
히든 노드라면 아래와 같이 계산한다.
$$ \delta_j = \omicron_j (1-\omicron_j)\sum_k{w_{jk}}\delta_k $$
가중치를 넣는 이유는 높은 가중치인 노드가 더 많은 책임이 있기 때문.
게인은 얼마나 학습이 빠르게 이뤄질지를 정한다. 이 값이 낮으면 안정적이지만 오래걸린다. 이 값이 높다면 빨리 학습하지만 불안정하다. (동작하지 않는다는 게 아니라 학습된 가중치들의 값이 튈 수 있음)
예시
대충 19개의 인풋이 있다고 가정하자. 여기에는 가장 가까운 적 5명과의 거리(5개), 가까운 아군 4명의 체력과 탄약 그리고 거리(12개), 그리고 나 자신의 체력과 탄약(2개)이 포함된다.
그리고 아웃풋은 4개가 있을 수 있다고 하자. 도망가기, 맞서싸우기, 동료를 치료하기, 적을 추적하기..
그리고 3개의 레이어를 사용한다고 가정해보자. 이중 두개는 인풋레이어와 아웃풋 레이어이다. 그리고 그 사이에 중간 레이어(혹은 히든 레이어)가 하나 있다.
- 인풋 레이어는 인풋 갯수와 동일한 갯수의 노드를 가지고 있다.(19개)
- 아웃풋 레이어 역시 아웃풋 갯수와 동일한 수의 노드를 가지고 있다 (4개).
- 중간 레이어는 보통 적어도 인풋 레이어의 노드 갯수만큼의 노드를 가지고 있다.
각 노드(perceptron)은 이전 레이어의 노드들에 대한 가중치를 가지고 있다. 인풋 레이어 값은 경우는 없다.
그리고 학습 데이터는 두 그룹 - 트레이닝 셋과 테스트 셋 - 으로 나눈다.
- 우선 모든 가중치를 매우 작은 임의의 값으로 초기화한다.
- 그리고 학습 알고리즘을 반복하며 데이터들을 순회한다.
- 각 반복마다 두가지를 수행한다. 하나는 Feedforward 그리고 Backpropagation.
반복이 끝나면 테스트셋으로 학습이 잘 이뤄졌는지 확인한다. 이 과정은 그냥 테스트셋을 feedforward하면 된다. 만약 학습이 잘 이뤄지지 않았다면 학습 데이터가 부족했거나, 학습데이터와 테스트 데이터의 유사도가 떨어지는 경우이다.
기타 기법들
아카데믹한 AI에서는 엄청난 기법들이 존재하지만 게임AI에서 적용할 만한 건 많지 않다. 그럼에도 3개정도는 사용을 고려해볼만 하다.
Radial Basis Function
Input이 특정 범위에 있도록 하고 싶은 경우에 쓴다. 이런 경우 역치 함수가 특정 범위에서 높은 값을 반환하도록 하면 된다. 그러나 단점으로 학습이 느려진다. 큰 네트워크에서는 Input이 특정 범위에 있도록 알아서 학습이 되는데, 중간 레이어 노드 중 하나가 하한치를 다른 하나가 상한치를 학습하기 때문이다. 그러나 이러면 네트워크 사이즈가 커지기 때문에 네트워크를 작고 효율적으로 운용하고 싶다면 쓸만하다.
Weakly Supervised Learning
위에서 든 인공신경망 학습 예시는 Supervised Learning이다. Backpropagation 과정에서 우리가 알고리즘에 정확한 정답을 주기 때문. Weakly Supervised Learning은 Unsupervised와는 다르다. 유저가 아닌 알고리즘이 학습에 정답을 준다는 차이가 있다. 이런 경우 보통 AI가 뭘 잘했다고 하는 것 보다 뭘 잘못했는지를 판별하게 하는 게 쉽다.(ex AI캐릭터의 사망 혹은 패배) 이렇게 알아서 학습하는 방식은 굉장히 흥미로워 보이지만... 개발자가 의도하지 않은 방향의 학습이 일어날 수 있다. (AI가 꼼수를 쓴다든지)
Hebbian Learning
이건 다른 인공 신경망들에 비해서 꽤 생물학적인 방법 중 하나이다. 꽤 실용적이며 구현도 간단하다. 이건 Unsupervised Learning으로 어떤 데이터나 피드백도 필요로 하지 않는다.
위에서 말한 MLP와의 차이점은, 헤비안 러닝은 layer대신에 노드가 격자 형태를 갖추고 있으며, 근처 이웃들과 연결되어 있다. 따라서 노드들은 이웃과 함께 활성화될 확률이 높다. 이 방식은 특정한 Output을 생성하기보다는 데이터에서 패턴을 찾는데 활용된다. (가령 RTS에서 위험지역을 판별하는 것)