개요
마르코프 시스템은 흔히 쓰는 명명법은 아니고, 그냥 마르코프 프로세스(Markov Process)를 쓰는 시스템이라는 뜻이다.
왜 쓰냐? 퍼지 상태 머신처럼 한 번에 여러 상태가 존재할 수 있는 것은 유용한데, 퍼지 상태 머신의 경우 각 상태의 소속도자체는 의미가 없고 상태들의 소속도를 적절히 역퍼지화(Defuzzify)해야 의미가 생긴다. 그러나 만약 상태들의 값 자체에 의미를 두고 싶은 경우에는 마르코프 프로세스를 이용할 수 있다.
마르코프 프로세스
과거는 무시하고 현재 상태로만 미래를 예측할 수 있는 경우를 다룬다.
대략적으로 설명하면 다음과 같다.
현재 날씨 상태를 표현하는 데이터가 있다고 하자.
어떤 날에 날씨가 맑다면 그 다음 날도 날씨가 맑을 확률이 0.8, 흐릴 확률이 0.2이다.
어떤 날에 날씨가 흐리다면 그 다음 날에 날씨가 맑을 확률은 0.3, 흐릴 확률은 0.7이라고 하자.
표로 나타내면 다음과 같다.
| 오늘/내일 | 맑음 | 흐림 |
| 맑음 | 0.8 | 0.2 |
| 흐림 | 0.3 | 0.7 |
이는 다시 전이행렬로 나타낼 수 있다.
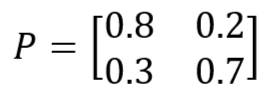
당연히 전이행렬의 각 행의 합은 1이 된다.
어떤 날 X에 통계적으로 날씨가 맑을 확률이 0.2, 흐릴 확률이 0.8이었다고 하자. 그러면 이틀 뒤의 날씨는 어떨까? 전이 행렬을 두 번 곱해주면 된다.

따라서 X의 이틀 뒤에 날씨가 맑을 확률은 0.5, 흐릴 확률은 0.5라는 결론을 내릴 수 있다.
마르코프 프로세스 활용
여기서는 굳이 벡터의 합이 1일 필요가 없다. 마찬가지로 전이 행렬의 각 행의 합도 1일 필요가 없다.
각 상태들의 값을 하나의 벡터로 표현할 수 있다. 이러한 벡터를 상태 벡터(state vector)라고 한다.
이제 상태 벡터에 알맞는 전이 행렬을 곱해준다면 다음 상태 벡터의 값을 알 수 있다.
예를 들어, 플레이어는 저격수이고 적을 저격할 수 있는 위치가 4군데 있다고 하자. 각 위치의 안전도는 다음과 같다.

이때, 플레이어가 첫 번째 위치에서 적을 저격한다면 첫 번째 위치의 안전도는 내려갈 것이지만 첫 번째 위치에 적의 이목이 집중되므로 다른 위치들의 안전도는 올라간다고 정할 수 있다. 그렇다면 첫 번째 위치에서 적을 저격하는 경우의 전이행렬을 다음과 같이 정의할 수 있다.

이제 여기에 상태 벡터V를 곱해주면 다음과 같은 결과가 나온다.

의도대로 첫 번째 위치의 안전도는 줄었지만 나머지 위치의 안전도는 증가했다. 전체적인 안전도는 4.0에서 3.4로 감소했다.
만약 플레이어가 계속 총을 쏜다면 전체적인 안전도는 계속 감소할 것이고 어떤 지역도 안전하지 않게 될 것이다.
이를 위해서 플레이어가 일정 시간동안 총을 쏘지 않는다면 전체적인 안전도를 증가시켜 줄 전이행렬을 정의해줄 수 있다.

이런 전이 행렬의 값들은 직접 조정하며 하나하나 입력해야 하지만 크게 어려운 작업은 아니다.
마르코프 상태 머신
조건을 만족하거나 이벤트가 발생하면 전이를 수행한다. 만약 어떤 조건도 만족하지 않았고 이벤트도 없다면 기본 전이(default transition)을 수행할 수 있다.
우선 전이들이 필요하다. 전이는 발동(trigger) 조건과 전이 행렬로 구성되어 있다.
전이는 개별적인 상태가 아니라 전체 상태 머신에 포함된다.
퍼지 상태 집합과 마찬가지로 상태가 행동을 결정하는게 아니라 전이가 행동을 결정한다.
class MarkovStateMachine :
//상태벡터
state : float[N]
//기본 전이 행렬을 수행할 시간
resetTime : int
//현재 카운트 다운
currentTime : int = resetTime
//모든 전이
transitions : MarkovTransitions[]
function update() -> Action[]:
//활성화 된 전이가 있는지 확인
triggeredTransition = null
for transition in transitions :
if transition.isTriggered() :
triggeredTransition = transition
break
//활성화된 전이가 있다.
if triggeredTransition :
currentTime = resetTime
matrix = triggeredTransition.getMatrix()
state = matrix * state
return triggerTransition.getActions()
//활성화된 전이가 없다. => 기본 전이를 수행한다.
else :
currentTime -= 1
if currentTime <= 0 :
state = defaultTransitionMatrix * state
currentTime = resetTime
return []참고 : Ian Millington, AI for GAMES 3rd edition, CRC press, [Chapter 5.6]
'Game AI' 카테고리의 다른 글
| 목표 지향 행동 - 2 (0) | 2022.11.24 |
|---|---|
| 목표 지향 행동 (Goal-Oriented Behavior) - 1 (0) | 2022.11.20 |
| 퍼지 상태 머신 (Fuzzy State Machine) (2) | 2022.11.02 |
| 퍼지 로직 의사 결정(Decision making) (0) | 2022.10.23 |
| 퍼지 로직(Fuzzy Logic) -2 (0) | 2022.10.03 |