곡선
곡선을 표현하기에 앞서, 두 정점 (A, B) 사이에 있는 점 P를 다음과 같이 표현할 수 있다.


또한 곡선은 t에 대한 방정식(P(t))으로 표현할 수 있다.

베지에 곡선(Bézier Curves)
n차 베지에 곡선은 n+1개의 점으로 얻을 수 있는 베지에 곡선이다.
1차(Linear) 베지에 곡선은 앞서 말한 점 A,B 사이에 있는 점 P의 집합으로 표현할 수 있다.

말이 곡선이지, 사실상 A-B를 잇는 선분이다.
2차(Quadratic) 베지에 곡선은 아래와 같다.

2차 베지에 곡선은 A와 B를 잇는 1차 베지에 곡선 위에 있는 한 점 AB(t)와 B와 C를 잇는 1차 베지에 곡선 위의 한 점 BC(t)사이에 있는 한 점 P(t)의 집합으로 볼 수 있다.

식으로 표현하면 다음과 같을 것이다.

이때 두 선분 AB와 BC의 길이가 다르다면 밀도(속도)의 차이가 발생할 수 있다.(비 균일성(Non-Uniformity)) 다시 말하면 t가 증가함에 따라 이동하는 거리가 차이 날 수 있다.

참고로 이런 밀도차이는 잘 이용하면 장점이 될 수 있는데, 예를 들어 A, B, C가 한 직선에 있으며 B, C의 길이가 A, B의 길이보다 더 긴 경우 A에 가까울수록 밀도가 높고, C에 가까울수록 밀도가 낮은 직선을 만들 수 있다. 이것을 이용하면 시작할 때는 느리게 가고 점점 빨라지는 직선 방정식을 만들 수 있다.
3차(Cubic) 베지에 곡선은 점 4개로 위 방법과 똑같이 하면 된다.

참고로 이런식으로 계산한 3차 베지어 곡선의 식은
$P(t) = s^3A + 3(s^2 t)B + 3(st^2)C + t^3D$ 이다.
n차 베지에 곡선은 위 방법에서 점의 개수만 늘려가면 된다. 그리고 보면 알겠지만 n차 베지에 곡선은 결국 t에 대한 n차 함수이다.
에르밋 곡선(Hermite Curve)
에르밋 곡선도 1차 2차.. n차가 있지만 검색해보니 3차 말고는 안 쓰는 듯하다.
3차 에르밋 곡선은 3차 베지에 곡선에서 변환 가능한 곡선인데, 4개의 점을 사용하는 대신 두 개의 벡터 U, V를 사용한다.

벡터 U와 V는 k*(B-A)와 k*(D-C)로 표현할 수 있다.

결국 에르밋 곡선은 베지에 곡선과 상호변환 가능하다. 즉, 베지에 곡선의 또 다른 표현 방법으로 봐도 무방할 것 같다.
변환 방법은 다음과 같다.
편의를 위해
$U=3(B-A), V=3(D-C)$
로 표현한다고 해보자.
이걸 다시 쓰면,
$B=A+U/3, C=D-V/3$
이다.
잘 정리하면,
$P(t) = s^2(1+2t) A + t^2(1+2s)D + s^2tU - st^2V$
으로 3차 에르밋 곡선을 표현할 수 있다.
참고로 행렬을 이용해서 표현할 수도 있는데, 모든 s에 $s=1-t$를 대입하면,

이렇게 쓸 수 있다.
행렬로 표현하면,

참고로 P(t)는 t에 대한 3차 함수이므로,
$P(t)=a_0+a_1t+a_2t^2+a_3t^3$
이렇게 표현할 수 있다.
이때, P(t)의 1차 도함수는
$P'(t)=a_1+2a_2t+3a_3t^2$
이며
$A=P(0), D=P(1), U=P'(0), V=P'(1)$
이렇게 표현하여 [A, D, U, V]를 각각 [P(0), P(1), P'(0), P'(1)]로 대체할 수 있다.
스플라인(Splines)
스플라인(Spline)은 곡선들이 서로의 양 끝점에 연결된 것이라고 할 수 있다. 이때 곡선들이 만나는 점을 Knot라 부른다.
베지에 곡선을 기반으로 한 베지에 스플라인과 에르밋 곡선을 기반으로 한 에르밋 스플라인이 존재한다.


베지에 곡선과 에르밋 곡선은 둘 다 t에 대한 매개변수 방정식인 P(t)로 표현했다. (t는 [0,1]) 그렇다면 여러 곡선이 모인 스플라인은 어떻게 표현해야 할까? 위의 그림처럼 3개의 곡선이 모인 스플라인이라면 t의 범위는 3배인 [0,3]이 된다. 그러면 t를 [0,1] , (1,2], (2,3]의 세 구간으로 나누어 1,2,3번 곡선에 차례대로 매칭 시켜주면 된다. 예를 들어 t=1.9라면 두 번째 곡선의 매개변수 값으로 0.9를 넣어주면 된다.
연속성(Continuity)
스플라인은 단순히 곡선을 연결하면 된다고 할 수 있겠지만, 자연스럽게 연결하기 위해서는 연속성에 대한 개념을 알아야 한다.
$C_0$ : 전체 곡선이 연속한다
$C_1$ : 곡선이 연속하고, 각 곡선이 만나는 곳의 접선 벡터가 같다. =0,1차 도함수가 연속이다. (미분 가능하다)

$C_2$ : 곡선이 연속하고, 접선 벡터가 같으며, 곡률이 같다. = 0,1,2차 도함수가 연속이다.
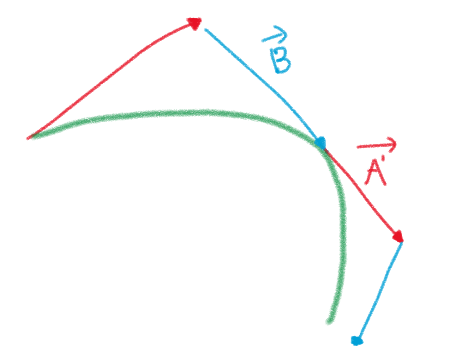
위 그림에서 B와 A'의 방향이 같다면 C1 연속을 만족한다. 만약 A'와 B의 속도(길이)도 같다면 C2연속을 만족한다.
C1연속은 좋은 곡선, C2 곡선은 완벽한 곡선이라 할 수 있다. (3차 스플라인인 경우)

캣멀롬(Catmull-Rom) 스플라인
3차 에르밋 스플라인의 경우 U, V 벡터를, 3차 베지에 스플라인의 경우 매개 정점 B,C를 매 곡선마다 정의해줘야 하니 매우 귀찮다.
그래서 U,V 벡터를 어떤 규칙으로 정하여 3차 에르밋 스플라인을 편하게 만드는 방법이 캣멀롬 스플라인이다.
캣멀롬 스플라인을 만드는 방법은 다음과 같다.
- 여러 정점 $P_0,P_1,P_2,...P_k$ 가 있다. 각 정점은 순서대로 연결된다.
- $P_0$의 시작 벡터(U)와, $P_k$의 끝 벡터는(V) 크기가 0이다.
- $P_n$의 V벡터와 $P_{n+1}$의 U벡터는 일치한다. (따라서 C2 연속이다.)
- $P_n$의 벡터는 $P_{n+1}-P_{n-1}$벡터를 2로 나눈 것이다.
예를 들면 다음과 같다.

위 그림처럼 순서대로 연결될 A,B,C,D 정점이 있다. A의 시작 벡터(U)의 속도는 0이라고 지정한다.

그 후 A, C 정점을 잇는 벡터를 2로 나눈 것을 B의 벡터로 정한다.

반복한다. D의 V벡터는 크기가 0이다.

위와 같은 3차 에르밋 스플라인이 완성되었다.
카디널 (Cardinal) 스플라인
카디널 스플라인은 캣멀롬 스플라인에 장력(tension)의 개념을 추가한 것이다. 적용 방법은 매우 간단한데, tension은 [0,1] 구간을 가지며 각 정점에서의 벡터 크기에 (1-tension)을 곱해주기만 하면 된다.

tension이 0인 경우에는 캣멀롬 스플라인과 같다.

tension이 0.5인 경우 각 벡터 크기는 절반이 된다.

tension 이 1.0인 경우 각 벡터의 속도가 0이므로 모두 직선이 된다.
기타 스플라인
Kochanek_Bartels(KB) 스플라인 : 카디널 스플라인에 Bias,와 Continuity를 추가한 것.
Basis Splines(B-Splines) : 베지에 스플라인의 한 종류로서 이웃 개념을 추가하여 곡선의 모양을 조절한 것.
기타
만약 베지어 곡선과 특정 점 사이에 거리를 구하고 싶다면 아래 글 참고
한 점과 가장 가까운 곡선 위의 점 구하기
※ 매개변수로 표현할 수 있는 곡선 (ex. 베지에 곡선)의 경우만 다룸. 관련 글 : 2021.07.11 - [이론] - 곡선(Curve) & 스플라인(Spline) 곡선(Curve) & 스플라인(Spline) 곡선 곡선을 표현하기에 앞서, 두 정점 (
tsyang.tistory.com
참고 : https://www.essentialmath.com/GDC2012/GDC12_Eiserloh_Squirrel_Interpolation-and-Splines.ppt
😑
'이론 > 그래픽스' 카테고리의 다른 글
| 컬링(Culling) (0) | 2021.12.14 |
|---|---|
| 배칭(Batching) (2) | 2021.11.15 |
| 드로우콜(Draw Call) (3) | 2021.11.13 |
| 병목(Bottleneck) (0) | 2021.11.03 |
| 렌더링 파이프라인 (1) | 2021.10.26 |