스트룸 정리 (Strum's theorem)

루트 격리 (root isolation)

---

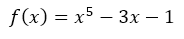
위 다항식의 실수 근을 구하는 알고리즘을 짜려면 어떻게 해야할까? 뉴턴 방법이나 이분 매칭 등을 써서 그 값을 구할 수 있지만 위와 같이 실근이 2개 이상인 경우 모든 실근을 구하는 방법은 꽤 고민이 된다.

 

그런데 이때, 만약 위 방정식의 실근이 구간 [-1.5, -1.0] , [-0.5, 0], [1.0, 1.5] 에 하나씩 있다는 정보가 주어진다면? 각 구간에 이분 매칭 혹은 뉴턴 방법을 사용한다면 매우 쉽게 모든 실근을 구할 수 있을 것이다. 이렇게 루트가 하나만 있는 구간을 구하는 것을 루트 격리(root isolation)라고 한다.

 

루트 격리는 여러 방법이 있는데 그 중 하나가 스트룸 정리이다. 

 

 

 

스트룸 정리(Strum's theorem)

---

스트룸 정리 (Strum's theorem)는 n차 다항식에서 어떤 구간에 실근(real roots)이 몇 개 있는지를 알아내는 방법을 제공한다. 이를 위해 스트룸 함수로 구성된 스트룸 체인(시퀀스)를 사용한다. 어떤 함수 $f(x)$에 대한 스트룸 함수 $f$는 다음과 같이 쓸 수 있다.

$f_n$은 $f_{n-2}$를 $f_{n-1}$로 나눈 나머지에 -1을 곱한 것이다. 

 

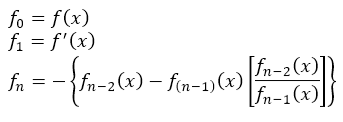
그럼 이걸 어떻게 써먹나? 예를 보면 이해하기 쉽다.

 

위에서 언급한 다항식이 있다.

 

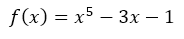
위 다항식의 스트룸 시퀀스를 구하면 다음과 같다.

 

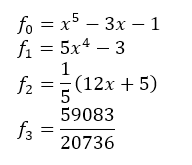
이제 $x$가 (-2, 0, 2)일 때 각 스트룸 함수값의 부호와 $d(x)$ 값을 알아보자. d는 스트룸 시퀀스에서 함수값의 부호가 바뀐 횟수이다. (0은 무시한다.)

 

 

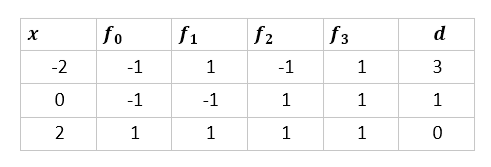
$x$가 -2일때는 부호가 3번 바뀌었으므로 (-1 -> 1, 1 -> -1, -1 -> 1) d의 값은 3이다.

 

자, 그럼 이 d값들을 어떻게 활용하는가?

$d(-2) - d(0) = 2$ 이다. 이것은 (-2,0]사이에 실근이 2개가 존재한다는 뜻이다.

마찬가지로 $d(0)-d(2)=1$ 이므로 (0,1]사이에는 실근이 하나 존재한다. 같은 방법으로 (-2,2]사이에는 실근이 3개 존재한다는 것을 알 수 있다. 그러나 (-2,0] 구간에 근이 두 개 이므로 루트 격리를 하지는 못했다. 따라서 저 구간을 반으로 나눈다면,

 

 

이제 (-2,-1] , (-1, 0], (0, 2] 구간에 루트가 하나씩 존재한다는 것을 알 수 있다.

 

우리가 근을 구하고자 했던 다항식의 그래프를 보면 루트 격리가 성공적임을 확인할 수 있다.

 

참고 :

https://mathworld.wolfram.com/SturmFunction.html

https://en.wikipedia.org/wiki/Sturm's_theorem