2021.08.13 - [수학] - 스트룸 정리 (Strum's theorem)
스트룸 정리 (Strum's theorem)
루트 격리 (root isolation) 위 다항식의 실수 근을 구하는 알고리즘을 짜려면 어떻게 해야할까? 뉴턴 방법이나 이분 매칭 등을 써서 그 값을 구할 수 있지만 위와 같이 실근이 2개 이상인 경우 모든
tsyang.tistory.com
목표 : 스트룸 정리를 이용하여 다항식의 해 찾기.
다항식 클래스
우선 다항식을 표현할 방법이 필요하여 Polynomial 클래스를 만들었다. Polynomial 클래스는
$a_0x^0 + a_1x^1+a_2x^2+ ... + a_nx^n$ 으로 표현되는 다항식의 각 계수 $(a_0, a_1, ... , a_n)$를 저장한다. 스트룸 정리에 필요한 기능으로는 다항식의 사칙연산과 미분 함수 구하기, 값 구하기 등이 있다.

테스트는 위와 같음.
개선점으로는 내부적으로 계산에만 사용되는 힙 메모리 할당이 생길 수 있는데 이부분은 풀링 해서 처리한다면 가비지가 쌓이는 것을 줄일 수 있을 듯.
대충 Polynomial 클래스를 어떻게 쓰는지 보기위해 테스트를 하나 가지고 왔다. 스트룸 정리에 많이 쓰이는 나머지 연산에 대한 테스트는 아래와 같다.
[Test]
public void PolynomialRemainderOpTest()
{
Polynomial a = new Polynomial(-1, -3, 0, 0, 0, 1); // -1 - 3x + x^5
Polynomial b = new Polynomial(-3, 0, 0, 0, 5); // -3 + 5x^4
var expected = a % b;
var actual = new Polynomial(-1, -2.4); // -1 -2.4x
Assert.AreEqual(expected.Equals(actual), true);
}
전체 테스트 코드
using System;
using System.Collections;
using System.Collections.Generic;
using NUnit.Framework;
using Src.Math;
public class PolynomialTest
{
[Test]
public void PolynomialEqualityTest()
{
Polynomial a = new Polynomial(new List<double>() { 0, 1, 2, 0});
Polynomial b = new Polynomial(0, 1, 2);
Assert.AreEqual(a.Equals(b), true);
Polynomial c = new Polynomial(1, 2, 3);
Polynomial d = new Polynomial(2, 2, 3);
Assert.AreEqual(c.Equals(d), false);
Polynomial e = new Polynomial(new List<double>());
Polynomial f = new Polynomial(0);
Assert.AreEqual(e.Equals(f), true);
}
[Test]
public void PolynomialDifferentiateTest()
{
Polynomial a = new Polynomial(-1, -3, 0, 0, 0, 1);
var differentiated = a.GetDifferentiated();
var truth = new Polynomial(-3, 0, 0, 0, 5);
Assert.AreEqual(differentiated.Equals(truth), true);
}
[Test]
public void PolynomialGetDegreeTest()
{
Polynomial a = new Polynomial(0, 1, ASFunc.DoubleEpsilon / 2.0);
Assert.AreEqual(a.Degree, 1);
Polynomial b = new Polynomial();
Assert.AreEqual(b.Degree, 0);
Polynomial c = new Polynomial(0, 1, ASFunc.DoubleEpsilon / 2.0, 3, 4);
Assert.AreEqual(c.Degree, 4);
}
[Test]
public void PolynomialDivideTest()
{
Polynomial n = new Polynomial(-1, -1, 0, 1, 1);
Polynomial d = new Polynomial(-1, 0, 3, 4);
(Polynomial p, Polynomial r) = Polynomial.Divide(n, d);
Polynomial calc = d * p + r;
Assert.AreEqual(calc.Equals(n), true);
}
[Test]
public void PolynomialRemainderOpTest()
{
Polynomial a = new Polynomial(-1, -3, 0, 0, 0, 1); // -1 - 3x + x^5
Polynomial b = new Polynomial(-3, 0, 0, 0, 5); // -3 + 5x^4
var expected = a % b;
var actual = new Polynomial(-1, -2.4); // -1 -2.4x
Assert.AreEqual(expected.Equals(actual), true);
}
[Test]
public void PolynomialQuotientOpTest()
{
Polynomial a = new Polynomial(-1, -3, 0, 0, 0, 1);
Polynomial b = new Polynomial(-3, 0, 0, 0, 5);
var expected = a / b;
var truth = new Polynomial(0, 0.2);
Assert.AreEqual(expected.Equals(truth), true);
}
[Test]
public void PolynomialMultiplyOpTest()
{
Polynomial a = new Polynomial(2, 3, 0, 1);
Polynomial b = new Polynomial(-1, 0, 1);
var expected = a * b;
var actual = new Polynomial(-2, -3, 2, 2, 0, 1);
Assert.AreEqual(expected.Equals(actual), true);
}
[Test]
public void PolynoimalAddOpTest()
{
var lhs = new Polynomial(0.5, 1.2, 0, 3.1);
var rhs = new Polynomial(0.1, 1.2, 5);
var expected = lhs + rhs;
var truth = new Polynomial(0.6, 2.4, 5, 3.1);
Assert.AreEqual(expected.Equals(truth), true);
}
[Test]
public void PolynoimalSubtractOpTest()
{
var lhs = new Polynomial(0.5, 1.2, 0, 3.1);
var rhs = new Polynomial(0.1, 1.2, 5);
var expected = lhs - rhs;
var truth = new Polynomial(0.4, 0, -5, 3.1);
Assert.AreEqual(expected.Equals(truth), true);
}
[Test]
public void PolynoimalNegativeSignOpTest()
{
var poly = new Polynomial(0.5, 1.2, 0, 3.1);
var expected = -poly;
var truth = new Polynomial(-0.5, -1.2, 0, -3.1);
Assert.AreEqual(expected.Equals(truth), true);
}
[Test]
public void PolynomialGetValueTest()
{
Polynomial f = new Polynomial(1, 1, 1, 1);
Assert.AreEqual(f.GetValue(2), 15);
Assert.AreEqual(f.GetValue(-2),-5);
Polynomial g = new Polynomial(3);
Assert.AreEqual(g.GetValue(-99),3);
}
[Test]
public void PolynomialGetTangentLineTest()
{
Polynomial f = new Polynomial(0, 0, 1); // y=x^2
var expected = f.GetTangentLine(2);
var actual = new Polynomial(-4, 4); // y = -4 + 4x;
Assert.AreEqual(expected.Equals(actual), true);
}
}전체 Polynomial 클래스 코드
using System;
using System.Collections.Generic;
namespace Src.Math
{
//a0 + a1*x^1 + a2*x^2 ... an*x^n 에서 (a0, a1, a2 , ... , an) 을 coefficients로 표현
public class Polynomial : IEquatable<Polynomial>, ICloneable
{
private List<double> m_Coefficients;
private int m_degree;
public int Degree => m_degree;
public Polynomial(List<double> coefficients)
{
m_degree = GetDegree(coefficients);
m_Coefficients = GetTrimmed(coefficients, m_degree);
}
public Polynomial(params double[] coefficients)
{
m_degree = GetDegree(coefficients);
m_Coefficients = GetTrimmed(coefficients, m_degree);
}
public Polynomial(in Polynomial other)
{
m_Coefficients = new List<double>(other.m_Coefficients);
m_degree = other.Degree;
}
public Polynomial GetDifferentiated()
{
var differentiatedCoef = new List<double>(m_Coefficients.Count - 1);
for (int i = 1; i < m_Coefficients.Count; ++i)
differentiatedCoef.Add(i * m_Coefficients[i]);
return new Polynomial(differentiatedCoef);
}
/// <summary>
/// 내부적으로 도함수를 구하므로, 한 객체에 이게 반복되어 사용 될 경우 오버로딩된 버전 사용할 것.
/// </summary>
public Polynomial GetTangentLine(double x)
{
return GetTangentLine(GetDifferentiated(), x);
}
//f1은 도함수
public Polynomial GetTangentLine(in Polynomial f1, double x)
{
double tangent = f1.GetValue(x);
double value = GetValue(x);
double constant = value - tangent * x;
return new Polynomial(constant, tangent);
}
public static Polynomial operator -(in Polynomial poly)
{
var newCoef = new List<double>(poly.m_Coefficients.Count);
for (int i = 0; i < poly.m_Coefficients.Count; ++i)
newCoef.Add(-poly.m_Coefficients[i]);
return new Polynomial(newCoef);
}
public static Polynomial operator +(in Polynomial lhs, in Polynomial rhs)
{
var biggerOne = lhs.m_Coefficients.Count > rhs.m_Coefficients.Count ?
lhs.m_Coefficients : rhs.m_Coefficients;
var smallerOne = ReferenceEquals(biggerOne, lhs.m_Coefficients) ?
rhs.m_Coefficients : lhs.m_Coefficients;
var newCoef = new List<double>(biggerOne.Count);
for (int i = 0; i < smallerOne.Count; ++i)
newCoef.Add(biggerOne[i]+smallerOne[i]);
for (int i = smallerOne.Count; i < biggerOne.Count; ++i)
newCoef.Add(biggerOne[i]);
return new Polynomial(newCoef);
}
public static Polynomial operator -(in Polynomial lhs, in Polynomial rhs)
{
return lhs + (-rhs);
}
public static (Polynomial, Polynomial) Divide(in Polynomial numerator, in Polynomial denominator)
{
if (numerator.Degree < denominator.Degree)
return (new Polynomial(0), numerator.Clone() as Polynomial);
var quotientCoefs = new List<double>(numerator.Degree - denominator.Degree + 1);
for (int i = 0; i < quotientCoefs.Capacity; ++i)
quotientCoefs.Add(0);
var remainderCoef = new List<double>(numerator.m_Coefficients);
int remainderDegree = numerator.Degree;
while (remainderDegree >= denominator.Degree)
{
int qDegree = remainderDegree - denominator.Degree;
double qCoef = remainderCoef[remainderDegree] / denominator.m_Coefficients[denominator.Degree];
quotientCoefs[qDegree] += qCoef;
for (int di = 0; di <= denominator.Degree; ++di)
remainderCoef[di + qDegree] -= denominator.m_Coefficients[di] * qCoef;
remainderDegree = GetDegree(remainderCoef);
}
return (new Polynomial(quotientCoefs), new Polynomial(remainderCoef));
}
public static Polynomial operator *(in Polynomial lhs, in Polynomial rhs)
{
int finalDegree = lhs.Degree + rhs.Degree;
var newCoef = new List<double>(finalDegree+1);
for (int i = 0; i <= finalDegree; ++i)
newCoef.Add(0);
for (int ri = 0; ri <= rhs.Degree; ++ri)
for (int li = 0; li <= lhs.Degree; ++li)
newCoef[ri + li] += rhs.m_Coefficients[ri] * lhs.m_Coefficients[li];
return new Polynomial(newCoef);
}
public static Polynomial operator /(in Polynomial lhs, in Polynomial rhs)
{
return Divide(lhs, rhs).Item1;
}
public static Polynomial operator %(in Polynomial lhs, in Polynomial rhs)
{
return Divide(lhs, rhs).Item2;
}
public double GetValue(double x)
{
double curX = 1.0;
double value = 0.0;
for (int i = 0; i < m_Coefficients.Count; ++i)
{
value += m_Coefficients[i] * curX;
curX *= x;
}
return value;
}
private static int GetDegree(IList<double> coefs)
{
int maxDegree = 0;
for (int i = 1; i < coefs.Count; ++i)
if(false == coefs[i].DoubleEqual(0f))
maxDegree = i;
return maxDegree;
}
private static List<double> GetTrimmed(IList<double> coefs, int degree)
{
List<double> newCoef = new List<double>(degree + 1);
if (coefs.Count == 0)
newCoef.Add(0);
else
{
for (int i = 0; i <= degree; ++i)
{
if(coefs[i].DoubleEqual(0d))
newCoef.Add(0d);
else
newCoef.Add(coefs[i]);
}
}
return newCoef;
}
public bool Equals(Polynomial other)
{
if (ReferenceEquals(null, other)) return false;
if (ReferenceEquals(this, other)) return true;
if (this.Degree != other.Degree) return false;
var thisSize = m_Coefficients.Count;
var otherSize = other.m_Coefficients.Count;
for (int i = 0; i <= this.Degree; ++i)
if (false == m_Coefficients[i].DoubleEqual(other.m_Coefficients[i]))
return false;
return true;
}
public override bool Equals(object obj)
{
if (ReferenceEquals(null, obj)) return false;
if (ReferenceEquals(this, obj)) return true;
if (obj.GetType() != this.GetType()) return false;
return Equals((Polynomial)obj);
}
public override int GetHashCode()
{
return (m_Coefficients != null ? m_Coefficients.GetHashCode() : 0);
}
public override string ToString()
{
return $"{nameof(m_degree)}: {m_degree}, {nameof(m_Coefficients)}: {ASFunc.ListElements2String(m_Coefficients)}";
}
public object Clone()
{
return new Polynomial(this);
}
//TODO : 내부적으로 연산할때 쓰이는 다항식의 경우 풀링을 해두고 사용하면 GC를 줄일 수 있을 듯
}
}
스트룸 체인 클래스(static)
스트룸 체인 클래스는 Static 클래스로 인자로 Polynomial 클래스를 받아서 스트룸 체인을 만들어주거나, 혹은 내부적으로 이것을 이용하여 주어진 구간에 루트 격리를 해주는 클래스이다.
[격리 구간의 최대 크기를 지정할 수 있는 루트격리 테스트]
[Test]
public void IsolateRootWithMaxSize()
{
double maxSize = 0.01;
var f = new Polynomial(1, -1, -1, 1);
var roots = new List<double>() { 1.0, -1.0 };
double min = -5, max = 5;
var isolatedRanges = StrumChain.IsolateRoot(f, min, max, maxSize);
foreach (var isolatedRange in isolatedRanges)
{
bool borderChecked = (isolatedRange.min >= min || isolatedRange.min.DoubleEqual(min)) &&
(isolatedRange.max <= max || isolatedRange.max.DoubleEqual(max)) &&
(isolatedRange.max - isolatedRange.min <= maxSize);
Assert.AreEqual(borderChecked, true);
}
foreach (var isolatedRange in isolatedRanges)
{
int numContainingRoots = 0;
foreach (var root in roots)
{
if (isolatedRange.min < root && root < isolatedRange.max || root.DoubleEqual(isolatedRange.max))
{
numContainingRoots++;
}
}
Assert.AreEqual(numContainingRoots, 1);
}
}
스트룸 체인의 경우 내부적으로 double타입의 사칙연산이 자주 발생하다 보니 아무래도 정확도에 대한 처리가 필요했다. 따라서 테스트의 경우 목표 정확도(0.000001)를 두어 오차가 목표 정확도 이내이면 정답으로 간주했다.
모든 스트룸 체인 테스트 코드
using System.Collections;
using System.Collections.Generic;
using NUnit.Framework;
using Src.Math;
using UnityEngine;
public class StrumChainTest
{
private const double TargetAccuracy = 0.000001;
[Test]
public void GetStrumChainTest()
{
//f = -1 - 1x + x^3 + x^4
var f = StrumChain.GetStrumChain(new Polynomial(-1, -1, 0, 1, 1));
var actualF = new List<Polynomial>();
actualF.Add(new Polynomial(-1, -1, 0, 1, 1)); // -1 - 1x + x^3 + x^4
actualF.Add(new Polynomial(-1, 0, 3, 4)); // -1 + 3x^2 + 4x^3
actualF.Add(new Polynomial(15.0 / 16.0, 3.0 / 4.0, 3.0 / 16.0)); // 15/16 + (3/4)x + (3/16)x^2
actualF.Add(new Polynomial(-64, -32)); // -64 -32x
actualF.Add(new Polynomial(-3.0 / 16.0)); // -3/16
Assert.AreEqual(f.Count, actualF.Count);
for (int i = 0; i < actualF.Count; ++i)
Assert.AreEqual(f[i].Equals(actualF[i]), true);
//g = -1 - 3x + x^5
var g = StrumChain.GetStrumChain(new Polynomial(-1, -3, 0, 0, 0, 1));
var actualG = new List<Polynomial>();
actualG.Add(new Polynomial(-1, -3, 0, 0, 0, 1)); // -1 - 3x + x^5
actualG.Add(new Polynomial(-3, 0, 0, 0, 5)); // -3 + 5x^4
actualG.Add(new Polynomial(1, 2.4)); // 1 + 2.4x
actualG.Add(new Polynomial(59083.0 / 20736.0)); // 59083.0/20736.0
Assert.AreEqual(g.Count, actualG.Count);
for (int i = 0; i < actualG.Count; ++i)
Assert.AreEqual(g[i].Equals(actualG[i]), true);
}
[Test]
public void GetSignChangeCountTest()
{
var f0 = new Polynomial(-1, -3, 0, 0, 0, 1);
var f1 = new Polynomial(-3, 0, 0, 0, 5);
var f2 = new Polynomial(1, 2.4);
var f3 = new Polynomial(59083.0 / 20736.0);
var strumChain = new List<Polynomial>{ f0, f1, f2, f3 };
Assert.AreEqual(StrumChain.GetSignChangeCount(strumChain, -2), 3);
Assert.AreEqual(StrumChain.GetSignChangeCount(strumChain, -1), 2);
Assert.AreEqual(StrumChain.GetSignChangeCount(strumChain, -0), 1);
Assert.AreEqual(StrumChain.GetSignChangeCount(strumChain, 2), 0);
var g0 = new Polynomial(1, -1, -1, 1); // 1 -x -x^2 + x^3
var g1 = new Polynomial(-1, -2, 3);
var g2 = new Polynomial(-8.0/9.0, 8.0/9.0);
var g3 = new Polynomial(0);
var strumChain2 = new List<Polynomial>{ g0, g1, g2, g3 };
Assert.AreEqual(StrumChain.GetSignChangeCount(strumChain2, -2), 2);
Assert.AreEqual(StrumChain.GetSignChangeCount(strumChain2, -1), 1);
Assert.AreEqual(StrumChain.GetSignChangeCount(strumChain2, 0), 1);
Assert.AreEqual(StrumChain.GetSignChangeCount(strumChain2, 1), 0);
Assert.AreEqual(StrumChain.GetSignChangeCount(strumChain2, 2), 0);
}
[Test]
public void GetSignChangeCountTestAccurate()
{
var f = new Polynomial(1, -1, -1, 1);
var strumChain = StrumChain.GetStrumChain(f);
int d1 = StrumChain.GetSignChangeCount(strumChain, 1d+TargetAccuracy);
int d2 = StrumChain.GetSignChangeCount(strumChain, 1d-TargetAccuracy);
Assert.AreEqual(d1, 0);
Assert.AreEqual(d2, 1);
}
[Test]
public void IsolateRootTest()
{
var f = new Polynomial(-1, -3, 0, 0, 0, 1);
var roots = new List<double>() { -1.21465, -0.334734, 1.38879 };
double min = -5, max = 5;
var isolatedRanges = StrumChain.IsolateRoot(f, min, max);
System.Action<List<DoubleRange>, List<double>, double, double> checkIsolatedRange = (isolatedRanges, roots, min, max) =>
{
foreach (var isolatedRange in isolatedRanges)
{
bool borderChecked = (isolatedRange.min >= min || isolatedRange.min.DoubleEqual(min)) &&
(isolatedRange.max <= max || isolatedRange.max.DoubleEqual(max));
Assert.AreEqual(borderChecked, true);
}
foreach (var isolatedRange in isolatedRanges)
{
int numContainingRoots = 0;
foreach (var root in roots)
if (isolatedRange.min < root && root < isolatedRange.max || root.DoubleEqual(isolatedRange.max))
numContainingRoots++;
Assert.AreEqual(numContainingRoots, 1);
}
};
Assert.AreEqual(isolatedRanges.Count, 3);
checkIsolatedRange(isolatedRanges, roots, min, max);
min = -2; max = 0;
isolatedRanges = StrumChain.IsolateRoot(f, min, max);
Assert.AreEqual(isolatedRanges.Count, 2);
checkIsolatedRange(isolatedRanges, roots, min, max);
min = 0; max = 1.3;
isolatedRanges = StrumChain.IsolateRoot(f, min, max);
Assert.AreEqual(isolatedRanges.Count, 0);
var g = new Polynomial(1, -1, -1, 1);
roots = new List<double>() { 1.0, -1.0 };
min = -3; max = 1;
isolatedRanges = StrumChain.IsolateRoot(g, min, max);
Assert.AreEqual(isolatedRanges.Count, 2);
checkIsolatedRange(isolatedRanges, roots, min, max);
}
[Test]
public void IsolateRootWithMaxSize()
{
double maxSize = 0.01;
var f = new Polynomial(1, -1, -1, 1);
var roots = new List<double>() { 1.0, -1.0 };
double min = -5, max = 5;
var isolatedRanges = StrumChain.IsolateRoot(f, min, max, maxSize);
foreach (var isolatedRange in isolatedRanges)
{
bool borderChecked = (isolatedRange.min >= min || isolatedRange.min.DoubleEqual(min)) &&
(isolatedRange.max <= max || isolatedRange.max.DoubleEqual(max)) &&
(isolatedRange.max - isolatedRange.min <= maxSize);
Assert.AreEqual(borderChecked, true);
}
foreach (var isolatedRange in isolatedRanges)
{
int numContainingRoots = 0;
foreach (var root in roots)
{
if (isolatedRange.min < root && root < isolatedRange.max || root.DoubleEqual(isolatedRange.max))
{
numContainingRoots++;
}
}
Assert.AreEqual(numContainingRoots, 1);
}
}
//스트럼 체인으로 목표 정확도 이내에 답을 구할 수 있는가. (최근 통과 속도 : 18ms)
[Test]
public void CalcRootWithStrumChain()
{
var f = new Polynomial(1, -1, -1, 1);
var roots = new List<double>() { 1.0, -1.0 };
double min = -10, max = 10;
var isolatedRanges = StrumChain.IsolateRoot(f, min, max, TargetAccuracy);
foreach (var isolatedRange in isolatedRanges)
{
bool success = false;
double mid = isolatedRange.Mid;
foreach (var root in roots)
{
if (mid.DoubleEqual(root, TargetAccuracy))
{
success = true;
break;
}
}
Assert.AreEqual(success, true);
}
}
}스트룸 체인 테스트 코드(미완성)
using System.Collections;
using System.Collections.Generic;
using Src.Math;
public static class StrumChain
{
public const double Tolerance = 0.000001;
public static List<Polynomial> GetStrumChain(in Polynomial f)
{
var strumChain = new List<Polynomial>();
strumChain.Add(new Polynomial(f));
if (f.Degree == 0) return strumChain;
var f1 = f.GetDifferentiated();
strumChain.Add(f1);
int curDegree = f1.Degree;
for (int i = 0; curDegree > 0; ++i)
{
var fi = -(strumChain[i] % strumChain[i + 1]);
strumChain.Add(fi);
curDegree = fi.Degree;
}
return strumChain;
}
public static int GetSignChangeCount(in List<Polynomial> strumChain, double x)
{
int changeCount = 0;
int curSign = 0;
for (int i = 0; i < strumChain.Count; ++i)
{
double val = strumChain[i].GetValue(x);
if (val.DoubleEqual(0.0))
continue;
int sign = val > 0 ? 1 : -1;
if (curSign * sign == -1)
changeCount++;
curSign = sign;
}
return changeCount;
}
/// <summary>
///
/// </summary>
/// <param name="min">exclusive</param>
/// <param name="max">inclusive</param>
/// <returns>오름차순으로 정렬된 루트 격리 범위를 반환 </returns>
public static List<DoubleRange> IsolateRoot(in Polynomial f, double min, double max, double maxSize = double.MaxValue)
{
var strumChain = StrumChain.GetStrumChain(f);
double mid = (min + max) / 2.0;
int minD, maxD;
minD = GetSignChangeCount(strumChain, min);
maxD = GetSignChangeCount(strumChain, max);
return RecursivelyIsolateRoot(strumChain, min, max, minD, maxD, maxSize);
}
private static List<DoubleRange> RecursivelyIsolateRoot(in List<Polynomial> strumChain,
double min, double max, int minD, int maxD, double maxSize)
{
var isolations = new List<DoubleRange>();
if (minD == maxD) return isolations;
if (minD - maxD == 1 && max-min < maxSize || max-min < Tolerance)
{
isolations.Add(new DoubleRange(min, max));
return isolations;
}
double mid = (min + max) / 2d;
int midD = GetSignChangeCount(strumChain, mid);
isolations.AddRange(RecursivelyIsolateRoot(strumChain, min, mid, minD, midD, maxSize));
isolations.AddRange(RecursivelyIsolateRoot(strumChain, mid, max, midD, maxD, maxSize));
return isolations;
}
/// <summary>
///
/// </summary>
/// <param name="min">exclusive</param>
/// <param name="max">inclusive</param>
/// <returns> 오름차순으로 정렬된 루트를 반환 </returns>
private static List<double> GetRootsInRange(in Polynomial f, double min, double max)
{
var rootIsolatedRanges = IsolateRoot(f, min, max);
List<double> roots = new List<double>(rootIsolatedRanges.Count);
var f1 = f.GetDifferentiated();
foreach(var rootIsolatedRange in rootIsolatedRanges)
roots.Add(GetRootInRange_Bisection(f, f1, rootIsolatedRange));
return roots;
}
}
해를 구하기 위한 구간 찾기(실패)
스트룸 체인으로 구간을 구하고 나면 뉴턴 방법 + 이분 탐색으로 다항식의 해를 구할 예정이었다. 속도가 빠른 뉴턴 방법으로 해를 구할 수 있다면 좋겠지만 그게 실패한다면 이분 탐색을 사용하게 된다. (실패의 여부는 뉴턴 방법이 주어진 루트 구간을 나가면 실패라고 간주.)
뉴턴 방법은 아래 움짤을 보면 어떤 건지 알 수 있다.
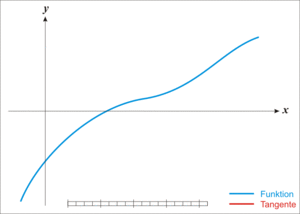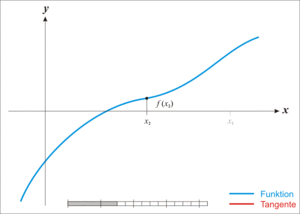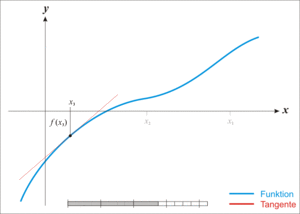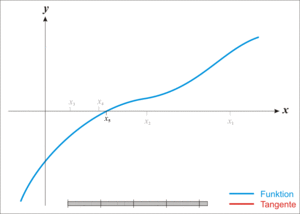
즉 나쁜 경우에 이분 탐색을 사용하게 되는데... 주어진 구간 내에서 증가만 or 감소만 하는 함수의 경우 무리없이 이분탐색을 할 수 있지만 중근을 가지는 경우가 매우 애매하다.

위 그래프에서 (0,3]이라는 루트 격리 구간을 얻는다면 이분 탐색도 삼분 탐색도 불가능해 보인다. (당연히 뉴턴 방법도 unstable 함)
즉 스트룸 체인으로 루트 격리를 할 때 안정성을 보장할 수 있는 구간을 주던지.. 혹은 뉴턴 방법이 무조건 성공하는 초기값을 주던지 해야 한다.
그리고 이 부분은 고민을 좀 해봐야 할 것 같다.
번외) 참고로 스트룸 정리만을 사용해서 다항식의 해를 구할 수 있다.
//스트럼 체인으로 목표 정확도 이내에 답을 구할 수 있는가. (최근 통과 속도 : 18ms)
[Test]
public void CalcRootWithStrumChain()
{
var f = new Polynomial(1, -1, -1, 1);
var roots = new List<double>() { 1.0, -1.0 };
double min = -10, max = 10;
var isolatedRanges = StrumChain.IsolateRoot(f, min, max, TargetAccuracy);
foreach (var isolatedRange in isolatedRanges)
{
bool success = false;
double mid = isolatedRange.Mid;
foreach (var root in roots)
{
if (mid.DoubleEqual(root, TargetAccuracy))
{
success = true;
break;
}
}
Assert.AreEqual(success, true);
}
}스트룸 체인을 구할 때 구간을 매우 잘게 쪼개면 된다. 속도도 의의로 빠르고 손으로 계산해보니 이분 탐색보다 느리긴 하지만 내가 주로 사용할 5차 다항식의 해를 구하는 용도라면 5배 이내로 차이 날 것 같다.
정 안되면 뉴턴 방법+스트룸구간 쪼개기로 루트를 구해도 될듯하다.